Skip to content

Chemical Reaction Networks Analysis and Catalyst Design

Reaction Networks

Chemical reaction networks have numerous different pathways to produce target molecules of interest. Solving the constrained combinatorial optimization problem of finding optimal reaction pathways has critical applications in synthesis planning and metabolic pathway analysis. This problem is generally a NP-hard problem due to the combinatorial explosion from the network graph size. A pre-print publication published by us, MQS, presents a benchmark between different solvers for reaction network analysis and the CP-SAT based approach has been implemented in the Cebule SDK which shows almost the same performance with respect to computational time (identical optimal minimum) in comparison to the best performing solver (Gurobi).

Mathematical Formulation

A chemical reaction network (CRN) can be represented as a bipartite directed graph with two types of nodes: reactions and species.

Each reaction in the network has associated costs:

  • Unit cost (unit_cost): Cost per quantity of the reaction (e.g., substrate purchase, byproduct disposal)
  • Fixed cost (fixed_cost): One-time cost incurred if the reaction occurs at all (e.g., equipment preparation)
  • Bounds: Lower (low) and upper (high) limits on reaction quantities

The optimization problem, as presented by Mizuno and Komatsuzaki, can be formulated as:

minimize: Σ(r∈R) [c_r^unit × x_r + c_r^fixed × p(x_r)]

subject to: 
  ∀s∈S: Σ(r∈R) v_{s,r} × x_r = 0  (mass balance)
  ∀r∈R: l_r ≤ x_r ≤ u_r           (reaction bounds)

Where:

  • R is the set of reactions, S is the set of species
  • x_r is the quantity of reaction r (optimization variable)
  • v_{s,r} is the signed stoichiometric coefficient of species s in reaction r
  • p(x_r) is the positivity indicator function (1 if x_r > 0, 0 otherwise)

Task Types

RXN_OPT

  • Optimize chemical reaction network pathways to minimize total cost while satisfying mass balance constraints
  • Inputs: crn_data: Dict[str, List[Dict]] containing the reaction network definition with keys reaction_list and species_list, time_limit: int maximum solve time in seconds
  • Cebule max_processors: Specify the number of cores to use
  • Output: Dict[str, Union[Dict[str, int], float, bool, Dict[str, float]]] containing the keys reaction_quantities (mapping reaction names to optimal quantities), total_cost (minimum total cost achieved), solve_time (total time taken in seconds), and optimal (whether optimal solution was found)

Input Format

Within crn_data dictionary:

  • reaction_list: Array of reaction definitions
  • name: Unique identifier for the reaction
  • fixed_cost: One-time cost if reaction occurs (≥0)
  • unit_cost: Cost per unit quantity of reaction (≥0)
  • low: Minimum allowed reaction quantity (≥0)
  • high: Maximum allowed reaction quantity (≥low)
  • species_list: Array of chemical species definitions
  • name: Unique identifier for the species
  • stoich: Dictionary mapping reaction names to signed stoichiometric coefficients
    • Positive values: species is produced by the reaction
    • Negative values: species is consumed by the reaction

Inflow and Outflow Reactions

Chemical reaction networks require boundary conditions to represent material inputs and product outputs. These are typically modeled as special reactions:

  • Inflow reactions: Represent external material supply (e.g., raw material purchases). These reactions have no reactants and produce species needed by the network. They should positive low bounds if the material is a required input to ensure minimum supply, but if the material is optional (ex. one pathway to produce the desired target includes it but not another) a positive lower bound should not be given.

  • Outflow reactions: Represent product extraction or waste disposal. These reactions consume species produced by the network and have no products. They may have positive low bounds to ensure minimum production targets are met. For species that require waste disposal (are byproducts or reactions but not required target chemicals) they should not have a positive lower bound.

Without inflow and outflow reactions, the mass balance constraints would force all reaction quantities to zero, as no net production or consumption would be possible in a closed system.

Example: Complete Solvay Process CRN

The following example details the Solvay Process CRN, shown in the below figure: 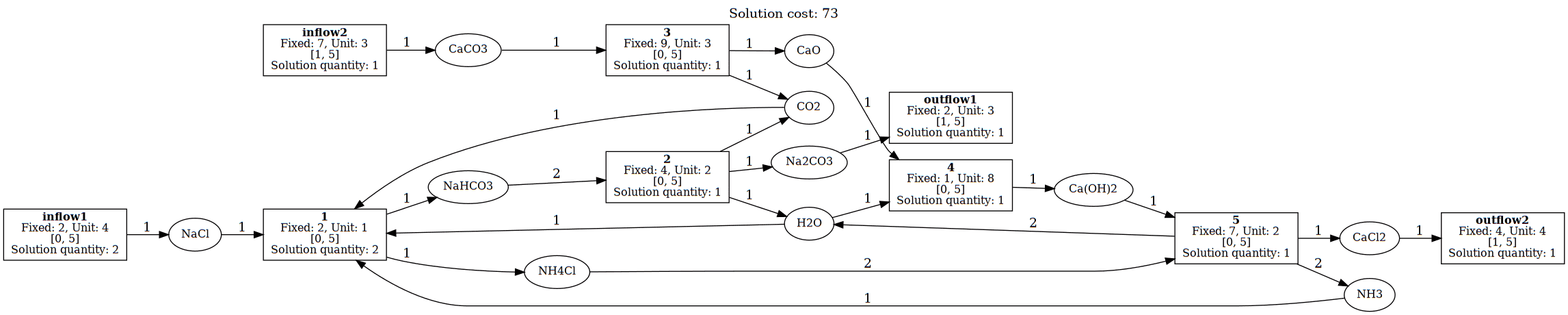Figure 1: Solvay Reaction Network with Optimal Solution Quantities

The input crn_data would be in the below format: 

{
  "reaction_list": [
    {
      "name": "inflow1",
      "fixed_cost": 2,
      "unit_cost": 4,
      "low": 0,
      "high": 5
    },
    {
      "name": "inflow2",
      "fixed_cost": 7,
      "unit_cost": 3,
      "low": 1,
      "high": 5
    },
    {
      "name": "1",
      "fixed_cost": 2,
      "unit_cost": 1,
      "low": 0,
      "high": 5
    },
    {
      "name": "2",
      "fixed_cost": 4,
      "unit_cost": 2,
      "low": 0,
      "high": 5
    },
    {
      "name": "3",
      "fixed_cost": 9,
      "unit_cost": 3,
      "low": 0,
      "high": 5
    },
    {
      "name": "4",
      "fixed_cost": 1,
      "unit_cost": 8,
      "low": 0,
      "high": 5
    },
    {
      "name": "5",
      "fixed_cost": 7,
      "unit_cost": 2,
      "low": 0,
      "high": 5
    },
    {
      "name": "outflow1",
      "fixed_cost": 2,
      "unit_cost": 3,
      "low": 1,
      "high": 5
    },
    {
      "name": "outflow2",
      "fixed_cost": 4,
      "unit_cost": 4,
      "low": 1,
      "high": 5
    }
  ],
  "species_list": [
    {
      "name": "NaCl",
      "stoich": {
        "inflow1": 1,
        "1": -1
      }
    },
    {
      "name": "CO2",
      "stoich": {
        "1": -1,
        "2": 1,
        "3": 1
      }
    },
    {
      "name": "NaHCO3",
      "stoich": {
        "1": 1,
        "2": -2
      }
    },
    {
      "name": "Na2CO3",
      "stoich": {
        "2": 1,
        "outflow1": -1
      }
    },
    {
      "name": "H2O",
      "stoich": {
        "1": -1,
        "2": 1,
        "4": -1,
        "5": 2
      }
    },
    {
      "name": "NH3",
      "stoich": {
        "1": -1,
        "5": 2
      }
    },
    {
      "name": "NH4Cl",
      "stoich": {
        "1": 1,
        "5": -2
      }
    },
    {
      "name": "CaCO3",
      "stoich": {
        "inflow2": 1,
        "3": -1
      }
    },
    {
      "name": "CaO",
      "stoich": {
        "3": 1,
        "4": -1
      }
    },
    {
      "name": "Ca(OH)2",
      "stoich": {
        "4": 1,
        "5": -1
      }
    },
    {
      "name": "CaCl2",
      "stoich": {
        "5": 1,
        "outflow2": -1
      }
    }
  ]
}

This represents the complete Solvay process with:

  • inflow1: NaCl supply (salt input)
  • inflow2: CaCO₃ supply (limestone input)
  • Reaction 1: Main ammonia-soda reaction: NaCl + CO₂ + H₂O + NH₃ → NaHCO₃ + NH₄Cl
  • Reaction 2: Sodium carbonate formation: 2 NaHCO₃ → Na₂CO₃ + CO₂ + H₂O
  • Reaction 3: Limestone calcination: CaCO₃ → CaO + CO₂
  • Reaction 4: Lime slaking: CaO + H₂O → Ca(OH)₂
  • Reaction 5: Ammonia recovery: Ca(OH)₂ + 2 NH₄Cl → 2 NH₃ + 2 H₂O + CaCl₂
  • outflow1: Na₂CO₃ product extraction
  • outflow2: CaCl₂ byproduct removal

Optimize reaction network with Cebule

# Create CRN optimization task
task_crn_opt = session.cebule.create_task(
    "Solvay Process Optimization",
    TaskType.RXN_NETWORK_OPT,
    crn_data=solvay_crn,
    time_limit=10
)

# Wait for result
result = session.cebule.wait_for_result(task_crn_opt.id, "result")
print(f"Optimal cost: {result['total_cost']}")
print(f"Reaction quantities: {result['reaction_quantities']}")
print(f"Optimization completed in {result['solve_time']} seconds")
print(f"Optimal solution found: {result['optimal']}")

Catalyst Design

Overview

The Catalyst Design module provides a comprehensive computational framework for designing and optimizing heterogeneous catalysts for chemical reactions. By combining quantum mechanical calculations with machine learning, the module enables:

  • High-throughput screening of bimetallic alloy surfaces
  • MLIP models wrapper and benchmarking to assess which machine learned interatomic potential model provides best results
  • Turnover Frequency (TOF) prediction using microkinetic modeling
  • Generative design of novel catalyst compositions using Generative Adversarial Networks (GANs)
  • Surface energy analysis through Wulff construction

The workflow follows an iterative optimization loop where catalyst candidates are generated, evaluated computationally, and refined through machine learning to discover high-performance materials.

Theoretical Background

Surface Reactions and Turnover Frequency

Heterogeneous catalysis occurs at the interface between a solid catalyst surface and gas-phase reactants. The catalytic activity is quantified by the Turnover Frequency (TOF), which represents the number of reaction cycles per active site per second.

The TOF depends on:

  1. Reaction energies (ΔE): Energy differences between reactants and products for each elementary step
  2. Activation barriers (Eₐ): Energy barriers that must be overcome for reactions to proceed
  3. Surface coverages (θ): Fraction of surface sites occupied by each adsorbate species
  4. Temperature (T) and Pressure (P): Thermodynamic conditions

Brønsted-Evans-Polanyi (BEP) Relation

Activation barriers are estimated using the BEP relation, which correlates the activation energy with the reaction energy:

Eₐ = α × ΔE + β

Where α and β are universal scaling parameters. For stepped transition metal surfaces 1: - α = 0.87 - β = 1.34 eV

Reaction Network Format

Reaction networks are defined in plain text files using the following syntax:

# Comment lines start with #
MOLECULE1 + 2*surf    --ER-->  2*ATOM1_fcc
MOLECUEL2 + 2*surf    --ER-->  2*ATOM2_bridge
MOLECULE3_ontop       --ads--> MOLECULE3 + surf

Syntax elements:

  • species_site: Adsorbate species at a specific surface site (e.g., ATOM1_fcc, ATOM2_bridge)

  • surf: Represents a vacant surface site

  • n*species: Stoichiometric coefficient (e.g., 2*ATOM1_fcc)

  • --ER-->: Eley-Rideal mechanism (gas-surface reaction)

  • --ads-->: Adsorption/desorption step

Supported adsorption sites: ontop, bridge, fcc, hcp, 3fold, 4fold

Supported Energy Calculators (includes MLIP, tight-binding and PW-DFT models)

Calculator Description
mace-mp MACE-MP machine learning potential
orb ORB machine learning potential
pet-mad PET-MAD potential
grace-2l-omat GRACE-2L potential
tblite GFN-xTB tight-binding DFT
pw-dft Plane-wave DFT

Task Types

MAKE_SURF

Generates a dataset of bimetallic alloy surfaces with randomized compositions.

Description: Creates catalyst surface structures by substituting atoms of a primary element with a secondary element at random positions. The surfaces can be FCC, stepped FCC (211), or stepped HCP structures, optionally with support materials.

Inputs:

Parameter Type Required Default Description
element1 str Yes - Primary element symbol (e.g., "Ru", "Pt")
element2 str Yes - Secondary element for alloying
surface_type str No "step_fcc" Surface structure: "fcc", "step_fcc", or "step_hcp"
n_surfaces int No 1 Number of unique surfaces to generate
lattice_const float Yes - Lattice constant of primary element [Å]
vacuum float No 10.0 Vacuum layer thickness [Å]
supercell_size_x int No 3 Supercell repetitions in x-direction
supercell_size_y int No 4 Supercell repetitions in y-direction
layers int No 3 Number of atomic layers
layers_to_fix int No 1 Bottom layers fixed during optimization
reaction_network dict Yes - Reaction network definition
dataset_tag str Yes - Unique identifier for the dataset

Optional Support Parameters:

Parameter Type Description
support str Support material formula (e.g., "OCeO" for ceria)
support_structure str Crystal structure: "fcc", "fluorite", "rocksalt", etc.
support_lattice_const float Support lattice constant [Å]
n_support_layers int Number of support layers
support_supercell_size_x int Support supercell size in x
support_supercell_size_y int Support supercell size in y

Output:

surf_config = {
    "surface_type": "step_fcc",
    "symbol": "ATOM1",
    "symbol2": "ATOM2",
    "vac": 10.0,
    "lattice_const": 2.7,
    "lateral_supercell_size": [3, 4],
    "nlayer": 3,
    "support_name": None,
    "support_lattice_const": None,
    "support_structure": None,
    "support_lateral_supercell_size": None,
    "support_nlayer": None,
    "layers_to_fix": 1,
}

Example with Cebule SDK:

from cebule import TaskType

# Create surface generation task
task_make_surf = session.cebule.create_task(
    "Generate ATOM1ATOM2 alloy surfaces",
    TaskType.MAKE_SURF,
    element1="ATOM1",
    element2="ATOM2",
    surface_type="step_fcc",
    n_surfaces=100,
    lattice_const=2.7,
    vacuum=10.0,
    layers=3,
    reaction_network=XY_network,
    dataset_tag="runi_screening_v1"
)

result = session.cebule.wait_for_result(task_make_surf.id, "result")
print(f"Generated {result['n_surfaces']} surface configurations")

GAS_SPECIES_ENERGY

Calculates reference energies for gas-phase species involved in the reaction network.

Description: Computes optimized geometries and total energies for all gas-phase molecules referenced in the reaction network. These serve as reference energies for computing adsorption and reaction energies.

Inputs:

Parameter Type Required Default Description
energy_calculator str Yes - Calculator type (see supported calculators)
optimizer_type str No "fire" Geometry optimizer: "fire", "lbfgs", "gpmin"
unitcell_length float No 12.0 Cubic unit cell size for gas molecules [Å]
temperature float No 700.0 Temperature for thermodynamic corrections [K]
pressure float No 100.0 Total pressure [bar]
dataset_tag str No - Associate results with a dataset
num_cores int No All Number of CPU cores to use

Output:

reaction_energies_gas = {
    "MOLECULE1": -16.45,   # Energy in eV
    "MOLECULE2": -6.77,
    "MOLECULE3": -19.82,
}

Example:

task_gas = session.cebule.create_task(
    "Calculate gas phase energies",
    TaskType.GAS_SPECIES_ENERGY,
    energy_calculator="mace-mp",
    temperature=700.0,
    pressure=100.0,
    dataset_tag="run_screening_1"
)

gas_energies = session.cebule.wait_for_result(task_gas.id, "result")

SURFACE_REACTION_ENERGIES

Calculates adsorption and reaction energies for all surfaces in a dataset.

Description: For each surface structure in the dataset, computes the energies of all adsorbate configurations defined in the reaction network, then calculates reaction energies (ΔE) for each elementary step.

Inputs:

Parameter Type Required Default Description
reaction_type dict Yes - Reaction network definition
temperature float No 700.0 Reaction temperature [K]
pressure float No 100.0 Total pressure [bar]
adsorbate_positions dict No - Override automatic adsorbate placement
backup_site list No - Fallback sites if primary fails
uncertainty bool No False Enable ensemble uncertainty quantification
fmax float No 0.05 Max force for geometry optimization [eV/Å]
dataset_tag str Yes - Dataset to process
num_cores int No All Number of CPU cores

For tblite calculator only:

Parameter Type Default Description
gfn int 2 GFN version (1 or 2)
electronic_temperature float 300.0 SCF smearing temperature [K]
geometry_opt bool False Refine with PW-DFT after tblite

Output:

reaction_energies_surf = {
    "surf_001": {
        "reaction_1": -0.82,  # dissociation ΔE [eV]
        "reaction_2": -0.45,  # dissociation
        "reaction_3": 0.12,   # Reaction 3
        "reaction_4": -0.23,  # Reaction 4
        "reaction_5": -0.15,  # Reaction 5
        "reaction_6": 0.67,   # Reaction 6
    },
    # ... additional surfaces
}

Example:

task_energies = session.cebule.create_task(
    "Calculate surface reaction energies",
    TaskType.SURFACE_REACTION_ENERGIES,
    reaction_type=reaction_network,
    temperature=400.0,
    pressure=50.0,
    uncertainty=True, # Enable kinetic uncertainty
    dataset_tag="run_screening_1"
)

# This task may take significant time for large datasets
result = session.cebule.wait_for_result(task_energies.id, "result", timeout=3600)

GAN_TOF

Trains a Generative Adversarial Network to discover high-performance catalyst compositions.

Description: Uses computed TOF values to train a conditional GAN that learns the relationship between atomic composition and catalytic activity. The generator produces new catalyst compositions optimized for the highest TOF class.

Inputs:

Parameter Type Required Default Description
reaction_type dict/str Yes - Reaction network or tag reference
dataset_tag str Yes - Dataset with computed TOF values
epochs int No 2000 Training epochs
nclass int No 5 Number of TOF classes for conditioning
score_max float No 5.0 Upper TOF outlier threshold (log₁₀ scale)
score_min float No -17.0 Lower TOF outlier threshold (log₁₀ scale)
scaler str No "standard" Data scaling: "standard" or "minmax"
min_loss_diff float No 1.0 Minimum G_loss - D_loss for successful training

Output:

surf_data = {
    "surfaces": [
        {
            "chemical_formula": "ATOMxATOMy",
            "atomic_numbers": [44, 44, 28, 44, ...],  # Per-atom composition
            "run": 3,  # GAN iteration number
        },
        # ... additional generated surfaces
    ],
    "training_loss": {
        "D_loss": [1.2, 0.8, 0.5, ...],
        "G_loss": [2.1, 1.5, 1.2, ...],
    }
}

Example:

# Run GAN optimization
task_gan = session.cebule.create_task(
    "GAN catalyst optimization",
    TaskType.GAN_TOF,
    reaction_type=reaction_network,
    dataset_tag="run_screening_1",
    epochs=3000,
    nclass=5,
    scaler="standard"
)

result = session.cebule.wait_for_result(task_gan.id, "result")
print(f"Generated {len(result['surfaces'])} new catalyst candidates")

# The new surfaces are automatically added to the dataset
# Run SURFACE_REACTION_ENERGIES again to evaluate them

Training Tips:

  1. Dataset size: Minimum ~80 surfaces recommended for effective training

  2. Class balance: Ensure reasonable distribution across TOF classes

  3. Convergence: Monitor that G_loss - D_loss > min_loss_diff

  4. Iteration: Repeat GAN → Energy calculation cycle until TOF converges

WULFF_CONSTRUCTION

Computes equilibrium crystal shape and surface energies using Wulff construction.

Description: Determines the thermodynamically stable crystal shape by calculating surface energies for all low-index Miller planes and constructing the Wulff shape. Optionally includes adsorbate effects on surface stability.

flowchart TD
    A[Generate all slabs up to Miller index 3] --> B

    subgraph loop["For each Miller index (hkl)"]
        B[Initialize N = 10 layers]
        B --> C[Compute slab energy E_slab]
        C --> D[Calculate surface energy γ = E_slab - N×E_bulk / 2A]
        D --> E{Adsorbate?}
        E -->|Yes| F[Add adsorbate, compute γ_ads]
        E -->|No| G[γ_final = γ]
        F --> G
        G --> H{Converged?<br/>Δγ ≤ 0.005 eV/Ų}
        H -->|No| I[N = N + 1]
        I --> C
        H -->|Yes| J[Record γ and hkl]
    end

    J --> K[Build Wulff polyhedron]
    K --> L[Output surface areas and energies]

Inputs:

Parameter Type Required Default Description
bulk str Yes - Element symbol for bulk structure
bulk_structure str Yes - Crystal structure: "fcc" or "hcp"
energy_calculator str Yes - Calculator for energy evaluation
reaction_type dict/str No - Include reaction network for TOF
adsorbate str No - Adsorbate species to include
site str No - Adsorption site (required if adsorbate set)
dataset_tag str Yes - Output dataset identifier

Optional Parameters:

Parameter Type Default Description
gas_species str - Gas molecule containing adsorbate
extra_gas_mol str - Additional gas reference
extra_gas_scalar float - Scaling for extra gas energy
backup_site str - Fallback adsorption site
md bool False Use NVT MD for energy
md_temperature float 700.0 MD temperature [K]
pressure float - Pressure for rate calculations [bar]
min_slab_size float 10.0 Minimum slab thickness [Å]
min_vacuum_size float 18.0 Minimum vacuum [Å]
fmax float 1000.0 Max force (large = no optimization)
compute_tof bool False Calculate TOF for each facet
num_cores int All CPU cores to use
surface_hull_tol float 1.5 Tolerance for surface atom detection

Output:

surf_energies = {
    "miller_indices": {
        (1, 1, 1): {
            "surface_energy": 0.092,  # eV/Ų
            "area_fraction": 0.45,
        },
        (1, 0, 0): {
            "surface_energy": 0.105,
            "area_fraction": 0.30,
        },
        (1, 1, 0): {
            "surface_energy": 0.098,
            "area_fraction": 0.25,
        },
    },
    "adsorption_energies": {  # If adsorbate specified
        (1, 1, 1): -0.82,
        (1, 0, 0): -0.75,
    },
    "tof_values": {  # If compute_tof=True
        (1, 1, 1): 1.2e-3,
        (1, 0, 0): 8.5e-4,
    },
    "activation_barriers": {
        (1, 1, 1): [0.87, 0.45, 0.92, 0.67, 0.55, 0.43],
    }
}

Example:

task_wulff = session.cebule.create_task(
    "Ru Wulff construction with N adsorbate",
    TaskType.WULFF_CONSTRUCTION,
    bulk="Atom1",
    bulk_structure="hcp",
    energy_calculator="mace-mp",
    adsorbate="Atom2",
    site="fcc",
    compute_tof=True,
    reaction_type=formation_network,
    dataset_tag="Atom2_wulff_analysis"
)

result = session.cebule.wait_for_result(task_wulff.id, "result")

# Access facet-specific information
for miller, data in result['miller_indices'].items():
    print(f"{miller}: γ = {data['surface_energy']:.3f} eV/Ų, "
          f"area = {data['area_fraction']*100:.1f}%")

VISUALIZE_SURF

Generates visualizations of catalyst surfaces with adsorbates.

Description: Creates 3D structural visualizations of catalyst surfaces, showing atomic positions, unit cells, and adsorbate configurations.

Inputs:

Parameter Type Required Default Description
catalyst_surface_tag str Yes - Dataset tag of surface to visualize
reaction_type dict/str Yes - Reaction network definition
adsorbate str No - Adsorbate to display
site str No - Adsorption site (required with adsorbate)
vacuum float No 10.0 Vacuum thickness [Å]
show_unit_cell bool No True Display unit cell boundaries
adsorbate_positions dict No - Manual position override
dataset_tag str Yes - Output identifier

Output: ASE Atoms object compatible with ase.visualize.view().

Example:

task_vis = session.cebule.create_task(
    "Visualize best catalyst",
    TaskType.VISUALIZE_SURF,
    catalyst_surface_tag="surf_042",  # Best performing surface
    reaction_type=formation_network,
    adsorbate="MOLECULE2",
    site="bridge",
    show_unit_cell=True,
    dataset_tag="run_screening_1"
)

atoms = session.cebule.wait_for_result(task_vis.id, "result")

# Use ASE visualization
from ase.visualize import view
view(atoms)

GAN

Analyzes GAN training progress and catalyst improvement over iterations.

Description: Generates analysis plots showing how catalyst performance (TOF) evolves across GAN training iterations.

Inputs:

Parameter Type Required Default Description
reaction_type dict/str Yes - Reaction network
dataset_tag str Yes - Dataset with GAN history
target_metric str No "TOF" Metric to track
score_max float No 5.0 Upper outlier threshold
score_min float No -17.0 Lower outlier threshold

Output: - Data structure for plotting TOF vs. GAN iteration - PNG/bytes object for direct visualization

Example:

task_gan_analysis = session.cebule.create_task(
    "Analyze GAN optimization progress",
    TaskType.GAN,
    reaction_type=formation_network,
    dataset_tag="run_screening_1",
    target_metric="TOF"
)

result = session.cebule.wait_for_result(task_gan_analysis.id, "result")


# Plot shows TOF improvement over GAN iterations
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(result['iterations'], result['mean_tof'], 'b-', label='Mean TOF')
plt.fill_between(result['iterations'], 
                 result['min_tof'], result['max_tof'], 
                 alpha=0.3, label='TOF range')
plt.xlabel('GAN Iteration')
plt.ylabel('log10(TOF)')
plt.legend()
plt.savefig('gan_progress.png')

POTENTIAL_ENERGY

Generates potential energy diagrams for reaction pathways.

Description: Creates energy profile plots showing the energetics of each elementary step along the reaction coordinate.

Inputs:

Parameter Type Required Default Description
reaction_type dict/str Yes - Reaction network
dataset_tag str Yes - Dataset with energy data

Output: - Data structure with ΔE values for each reaction step - PNG/bytes object for the energy diagram

Example:

task_ped = session.cebule.create_task(
    "Generate potential energy diagram",
    TaskType.POTENTIAL_ENERGY,
    reaction_type=reaction_network,
    dataset_tag="run_screening_1"
)

result = session.cebule.wait_for_result(task_ped.id, "result")

# Result contains energy levels for each state along reaction path
print("Reaction energies [eV]:")
for step, energy in result['reaction_energies'].items():
    print(f"  {step}: ΔE = {energy:+.3f}")

FRACTIONAL_COVERAGES

Analyzes surface coverage distributions across multiple catalyst surfaces.

Description: Computes and compares the fractional surface coverages of all adsorbate species under reaction conditions for multiple catalyst surfaces.

Inputs:

Parameter Type Required Default Description
reaction_type dict/str Yes - Reaction network
dataset_tag_list list Yes - List of dataset tags to compare

Output: - Coverage data for each species on each surface - Visualization comparing coverage distributions

Example:

task_coverage = session.cebule.create_task(
    "Compare surface coverages",
    TaskType.FRACTIONAL_COVERAGES,
    reaction_type=nh3_formation_network,
    dataset_tag_list=["TAG1", "TAG2", "TAG3"]
)

result = session.cebule.wait_for_result(task_coverage.id, "result")

# Access coverage data
for dataset, coverages in result['coverages'].items():
    print(f"\n{dataset}:")
    for species, theta in coverages.items():
        print(f"  θ({species}) = {theta:.4f}")

REACTION_ENERGIES_COMPARISON

Compares reaction energies across different surfaces or calculation methods.

Description: Generates statistical comparisons of reaction energies, useful for validating computational methods or comparing catalyst families.

Inputs:

Parameter Type Required Default Description
reaction_type dict/str Yes - Reaction network
dataset_tag str Yes - Dataset for comparison

Output: - Statistical metrics (mean, max, min differences) for each reaction - Comparison visualization

Example:

task_compare = session.cebule.create_task(
    "Compare reaction energies across methods",
    TaskType.REACTION_ENERGIES_COMPARISON,
    reaction_type=reaction_network,
    dataset_tag="method_comparison_v1"
)

result = session.cebule.wait_for_result(task_compare.id, "result")

print("Reaction energy comparison:")
print(f"  Overall mean difference: {result['overall_mean']:.3f} eV")
print(f"  Overall max difference:  {result['overall_max']:.3f} eV")
print(f"  Overall min difference:  {result['overall_min']:.3f} eV")

Complete Workflow Example

The following example demonstrates a complete catalyst optimization workflow for a reaction network which can adapted:

from cebule import Session, TaskType

# Initialize session
session = Session()

# Define reaction network
reaction_network = {
    "name": "example_rx",
    "reactions": [
    "MOLECULE1 + 2*surf --ER-->  2*ATOM1_fcc",
        "MOLECUEL2 + 2*surf --ER-->  2*ATOM2_bridge",
        "MOLECULE3_ontop --ads--> MOLECULE3 + surf"
    ]
}

DATASET_TAG = "run_optimization_1"

# Step 1: Generate initial catalyst surfaces
task_surf = session.cebule.create_task(
    "Generate ATOM1ATOM2 surfaces",
    TaskType.MAKE_SURF,
    element1="ATOM1",
    element2="ATOM1",
    surface_type="step_fcc",
    n_surfaces=100,
    lattice_const=2.7,
    layers=3,
    reaction_network=reaction_network,
    dataset_tag=DATASET_TAG
)
session.cebule.wait_for_result(task_surf.id, "result")

# Step 2: Calculate gas-phase reference energies
task_gas = session.cebule.create_task(
    "Gas phase energies",
    TaskType.GAS_SPECIES_ENERGY,
    energy_calculator="mace-mp",
    temperature=700.0,
    pressure=100.0,
    dataset_tag=DATASET_TAG
)
session.cebule.wait_for_result(task_gas.id, "result")

# Iterative GAN optimization loop
for iteration in range(5):
    print(f"\n=== GAN Iteration {iteration + 1} ===")

    # Step 3: Calculate surface reaction energies
    task_energies = session.cebule.create_task(
        f"Surface energies (iter {iteration})",
        TaskType.SURFACE_REACTION_ENERGIES,
        reaction_type=reaction_network,
        temperature=700.0,
        pressure=100.0,
        dataset_tag=DATASET_TAG
    )
    session.cebule.wait_for_result(task_energies.id, "result", timeout=7200)

    # Step 4: Train GAN and generate new candidates
    task_gan = session.cebule.create_task(
        f"GAN training (iter {iteration})",
        TaskType.GAN_TOF,
        reaction_type=reaction_network,
        dataset_tag=DATASET_TAG,
        epochs=2000,
        nclass=5
    )
    result = session.cebule.wait_for_result(task_gan.id, "result")

    print(f"Generated {len(result.get('surfaces', []))} new candidates")

# Step 5: Generate final analysis
task_analysis = session.cebule.create_task(
    "Final GAN analysis",
    TaskType.GAN,
    reaction_type=reaction_network,
    dataset_tag=DATASET_TAG
)
analysis = session.cebule.wait_for_result(task_analysis.id, "result")

# Step 6: Visualize best catalyst
task_ped = session.cebule.create_task(
    "Energy diagram for best catalyst",
    TaskType.POTENTIAL_ENERGY,
    reaction_type=reaction_network,
    dataset_tag=DATASET_TAG
)
session.cebule.wait_for_result(task_ped.id, "result")

print("\nOptimization complete!")
print(f"Best TOF achieved: {analysis['best_tof']:.2e}")
print(f"Best composition: {analysis['best_composition']}")

  1. J.K. Nørskov, T. Bligaard, A. Logadottir, S. Bahn, L.B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl, and C.J.H. Jacobsen. Universality in heterogeneous catalysis. Journal of Catalysis, 209(2):275–278, 2002. doi:https://doi.org/10.1006/jcat.2002.3615. ↩